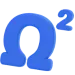Уравнения равновесия балки: пошаговый мастер-класс
Основа любого расчета в сопромате — определение реакций опор. Без них невозможно построить эпюры и проверить прочность. В этой статье мы разберем, как составить и решить три главных уравнения статики для любой балки.
Три нерушимых закона статики
Чтобы балка находилась в покое, она должна подчиняться трем фундаментальным условиям равновесия:
\( \sum F_x = 0 \)
Сумма всех горизонтальных сил равна нулю.
\( \sum F_y = 0 \)
Сумма всех вертикальных сил равна нулю.
\( \sum M_A = 0 \)
Сумма моментов всех сил равна нулю.
Шаг 1: Освободите балку — создайте расчетную схему
Первый и самый важный шаг — мысленно «убрать» опоры, заменив их действие силами-реакциями. Это называется созданием схемы свободных тел.
- Шарнирно-неподвижная опора (A): Запрещает движение по горизонтали и вертикали. Заменяется двумя реакциями: \(R_{Ax}\) и \(R_{Ay}\).
- Шарнирно-подвижная опора (B): Запрещает движение только по вертикали. Заменяется одной реакцией: \(R_{B}\).
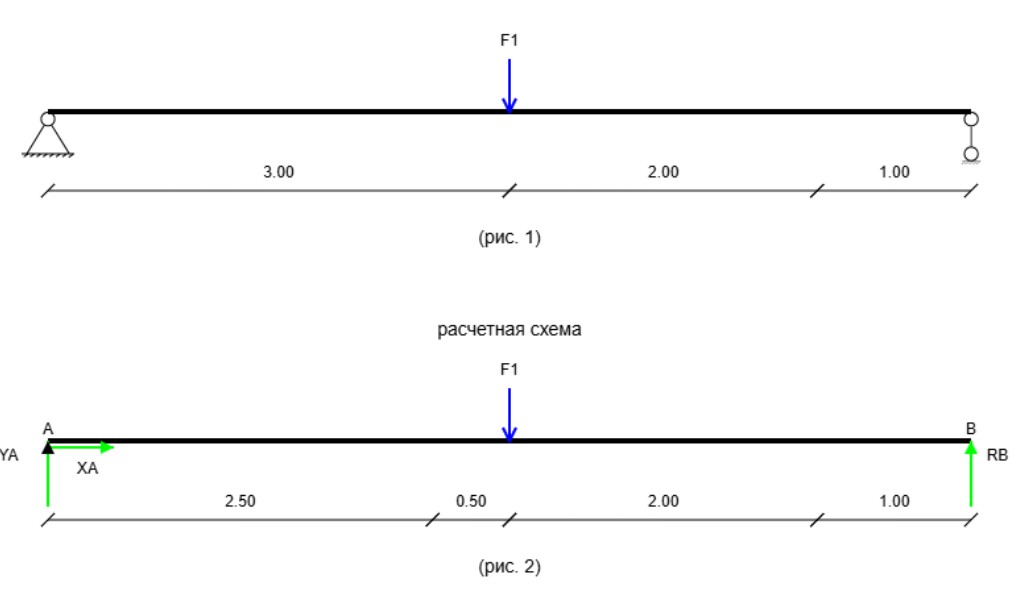
Мы не знаем, куда на самом деле направлены реакции — мы это предполагаем. Если в расчете получится отрицательное значение (например, \(R_{Ay} = -50\) кН), это просто значит, что реальное направление силы противоположно нарисованному.
Шаг 2: Установите «правила игры» — правило знаков
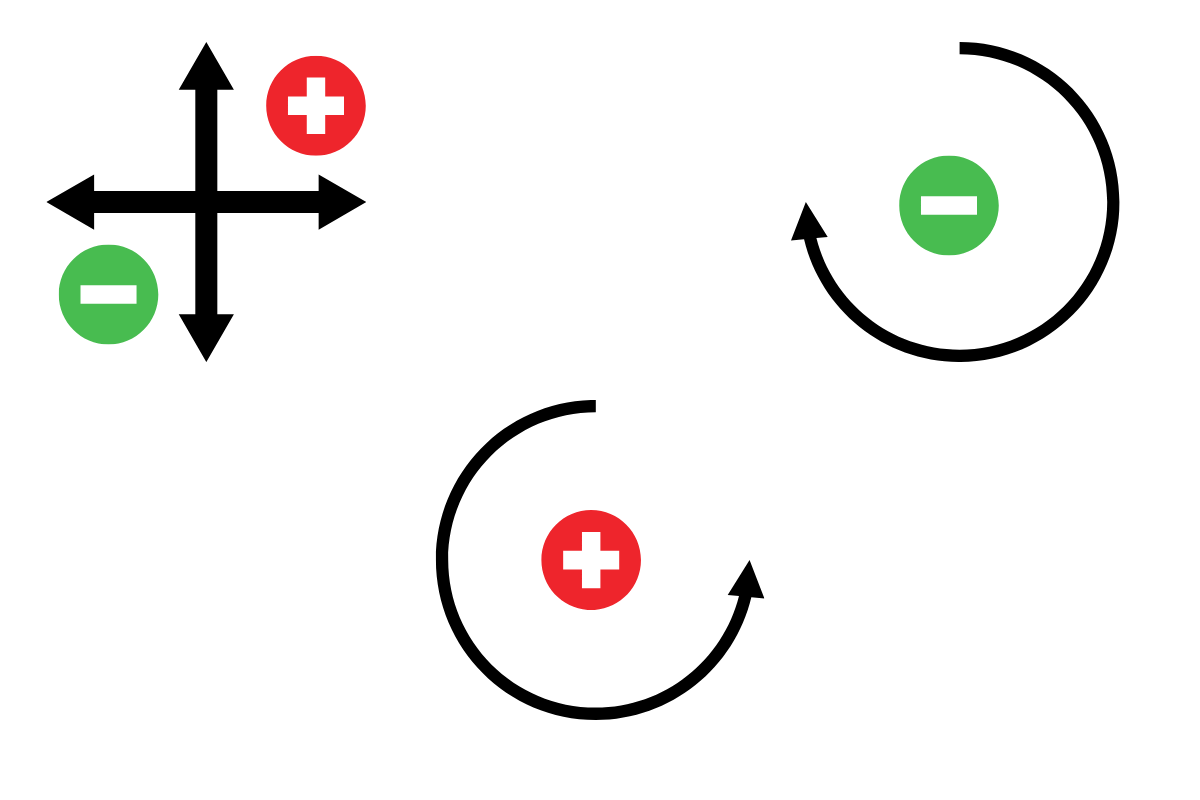
Чтобы избежать путаницы, в инженерной практике приняты единые правила знаков:
Для сил:
- Направленные вправо и вверх — положительные (+).
- Направленные влево и вниз — отрицательные (-).
Для моментов:
- Вращающие против часовой стрелки — положительные (+).
- Вращающие по часовой стрелке — отрицательные (-).
Шаг 3: Составляем и решаем уравнения
Применим теорию на практике: балка длиной 6 м, с силой F=20 кН посередине.
1. Сумма моментов \( \sum M_A = 0 \)
Лайфхак: всегда начинайте с уравнения моментов относительно опоры, где больше неизвестных (здесь — точка А). Так \(R_{Ax}\) и \(R_{Ay}\) не войдут в уравнение. Помним: Момент = Сила × Плечо.
\( -F \cdot 3 + R_B \cdot 6 = 0 \)
\(-20 \cdot 3 + R_B \cdot 6 = 0 \Rightarrow 6 \cdot R_B = 60 \)
\( \Rightarrow R_B = 10 \) кН
2. Сумма горизонтальных сил \( \sum F_x = 0 \)
Ищем все горизонтальные силы. В нашем случае она только одна.
\( R_{Ax} = 0 \)
\( \Rightarrow R_{Ax} = 0 \) кН
3. Сумма вертикальных сил \( \sum F_y = 0 \)
Суммируем все вертикальные силы, подставляя уже найденную \( R_B \).
\( R_{Ay} — F + R_B = 0 \)
\( R_{Ay} — 20 + 10 = 0 \Rightarrow R_{Ay} — 10 = 0 \)
\( \Rightarrow R_{Ay} = 10 \) кН

Шаг 4: Золотое правило инженера — проверка
Чтобы быть на 100% уверенным в расчете, составим уравнение моментов относительно другой точки, например, B. Если мы все сделали правильно, получится ноль.
\( \sum M_B = R_{Ay} \cdot 6 — F \cdot 3 \)
\( 10 \cdot 6 — 20 \cdot 3 = 60 — 60 = 0 \)
0 = 0. Расчет верен!
От теории к практике за секунды
Ручной расчет — отличный способ понять механику. Но для сложных задач, где много нагрузок, лучше довериться автоматике. Наш калькулятор моментально найдет реакции опор и построит эпюры.
Рассчитать реакции опор онлайн