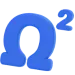Расчет опасного сечения балки на прочность
Любая балка под нагрузкой имеет «слабое звено» — сечение, где материал испытывает максимальное напряжение. Наша задача — найти его и убедиться, что оно выдержит. Это ключевой этап в обеспечении безопасности любой конструкции.
Почему момент — это ключ к прочности?
Разрушение балки вызывают нормальные напряжения (\(\sigma\)). Их величина в любой точке напрямую зависит от изгибающего момента (M) в этой же точке. Связь описывается главной формулой сопромата:
Вывод прост: где максимальный момент, там и максимальные напряжения. Именно это место мы и называем опасным сечением.
Шаг 1: Постройте эпюру изгибающих моментов (M)
Эпюра M — это ваш основной инструмент. Она представляет собой график, который наглядно показывает, как меняется изгибающий момент по длине балки. Чтобы ее получить, нужно провести статический расчет: найти реакции опор и вывести уравнения для моментов.
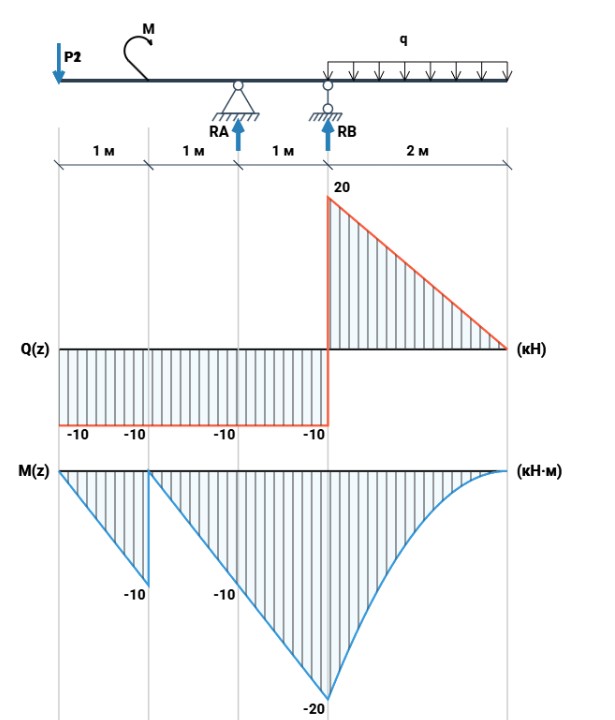
Шаг 2: Найдите Mmax — максимальный момент по модулю
Теперь самое главное. Ваша задача — найти на эпюре точку, наиболее удаленную от нулевой линии, неважно, вверх (положительные значения) или вниз (отрицательные значения).
Золотое правило инженера:
Опасность сечения определяется абсолютным значением (модулем) момента. Момент -200 кН·м так же опасен, как и +200 кН·м.
Алгоритм поиска:
- Найдите на эпюре самый большой положительный «пик».
- Найдите на эпюре самый большой отрицательный «провал».
- Сравните их абсолютные значения (модули). То, которое больше, и будет вашим \(M_{max}\).
Шаг 3: Выполните проверку на прочность
Это финальный и самый ответственный этап. Мы должны убедиться, что материал балки в самом напряженном месте сможет выдержать нагрузку.
Что такое условие прочности?
Для каждого материала (сталь, дерево, бетон) существует предельное напряжение, которое он может выдержать. С учетом запасов прочности инженеры используют допускаемое напряжение (обозначается \([\sigma]\)). Наша задача — проверить, чтобы максимальное напряжение в балке (\(\sigma_{max}\)) не превышало это безопасное значение.
\( \sigma_{max} \le [\sigma] \)
Как провести расчет?
Мы объединяем две формулы в одну:
- Берем найденное на Шаге 2 значение \(|M_{max}|\).
- Находим для сечения балки момент сопротивления \(W_x\) (он зависит от формы и размеров: для прямоугольника \(bh^2/6\), для круга \(\pi d^3/32\)).
- Рассчитываем фактическое максимальное напряжение: \( \sigma_{max} = \frac{|M_{max}|}{W_x} \).
- Сравниваем результат с допускаемым напряжением \([\sigma]\) из справочников для вашего материала.
Если \( \sigma_{max} \le [\sigma] \):
Отлично! Условие прочности выполняется. Ваша балка спроектирована правильно и выдержит заданную нагрузку.
Если \( \sigma_{max} > [\sigma] \):
Тревога! Прочность не обеспечена. Необходимо либо увеличить размеры сечения (что увеличит \(W_x\)), либо выбрать более прочный материал (с большим \([\sigma]\)).
Частая ошибка: почему знак момента не важен для прочности?
Начинающие инженеры иногда сравнивают значения, а не их модули (считая, что +50 кН·м «лучше», чем -80 кН·м). Это неверно. Знак момента указывает лишь на то, какие волокна растянуты (при M > 0 — нижние, при M < 0 — верхние). Прочность же материала на растяжение и сжатие в расчетах часто принимается одинаковой, поэтому для оценки опасности важна только абсолютная величина напряжения.
Устали от ручных расчетов?
Наш онлайн-калькулятор не просто строит эпюры Q и M, но и автоматически находит опасные сечения, выполняет проверку прочности и помогает подобрать сечение. Сэкономьте время и будьте уверены в результате.
Рассчитать балку онлайн