Как определить уравнение траектории точки
В задачах по кинематике движение точки часто описывается параметрическими уравнениями. Они показывают, где находится точка в любой момент времени \(t\). Но как выглядит сам путь? Чтобы ответить на этот вопрос, нужно найти уравнение траектории — то есть, зависимость \(y(x)\), исключив время.
Основной метод: исключение параметра \(t\)
Главная идея очень проста: выразить время \(t\) из одного уравнения и подставить его во второе. Однако для разных типов функций существуют свои хитрости. Рассмотрим три классических случая.
Пример 1: Степенные функции
Это самый простой и распространенный случай, который решается по стандартному алгоритму.
Условие:
\( x(t) = 2t + 1 \)
\( y(t) = 4t^2 — 3 \)
Шаг 1: Выражаем \(t\) из уравнения для \(x(t)\).
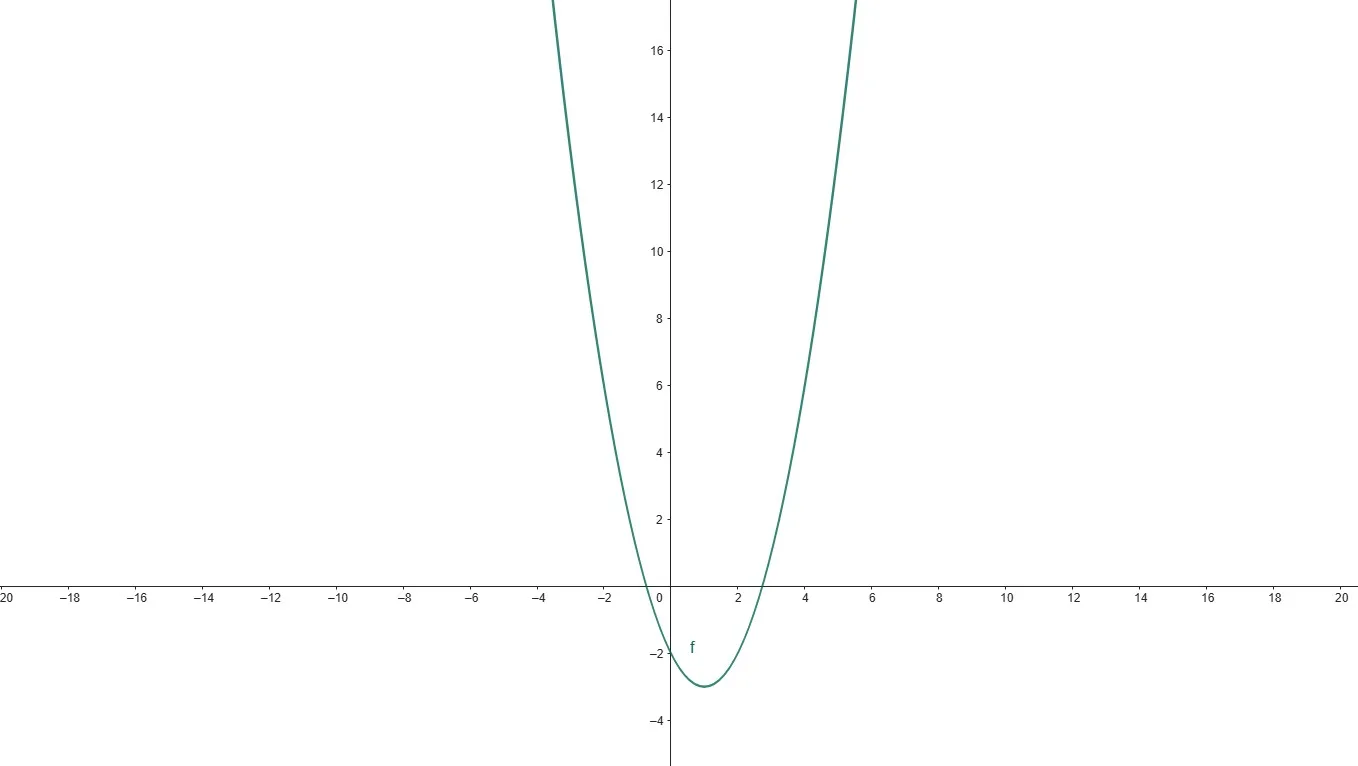
\( x = 2t + 1 \Rightarrow 2t = x — 1 \Rightarrow t = \frac{x-1}{2} \)
Шаг 2: Подставляем это выражение в уравнение для \(y(t)\).
\( y = 4 \left( \frac{x-1}{2} \right)^2 — 3 = 4 \frac{(x-1)^2}{4} — 3 = (x-1)^2 — 3 \)
Результат: Уравнение траектории — \( y = (x-1)^2 — 3 \). Это парабола.
Пример 2: Тригонометрические функции
Здесь прямой метод сложен. Гораздо проще использовать основное тригонометрическое тождество.
Условие:
\( x(t) = 5\cos(t) \)
\( y(t) = 3\sin(t) \)
Ключевая идея:
\( \sin^2(t) + \cos^2(t) = 1 \)
Шаг 1: Выражаем \(\cos(t)\) и \(\sin(t)\) из каждого уравнения.
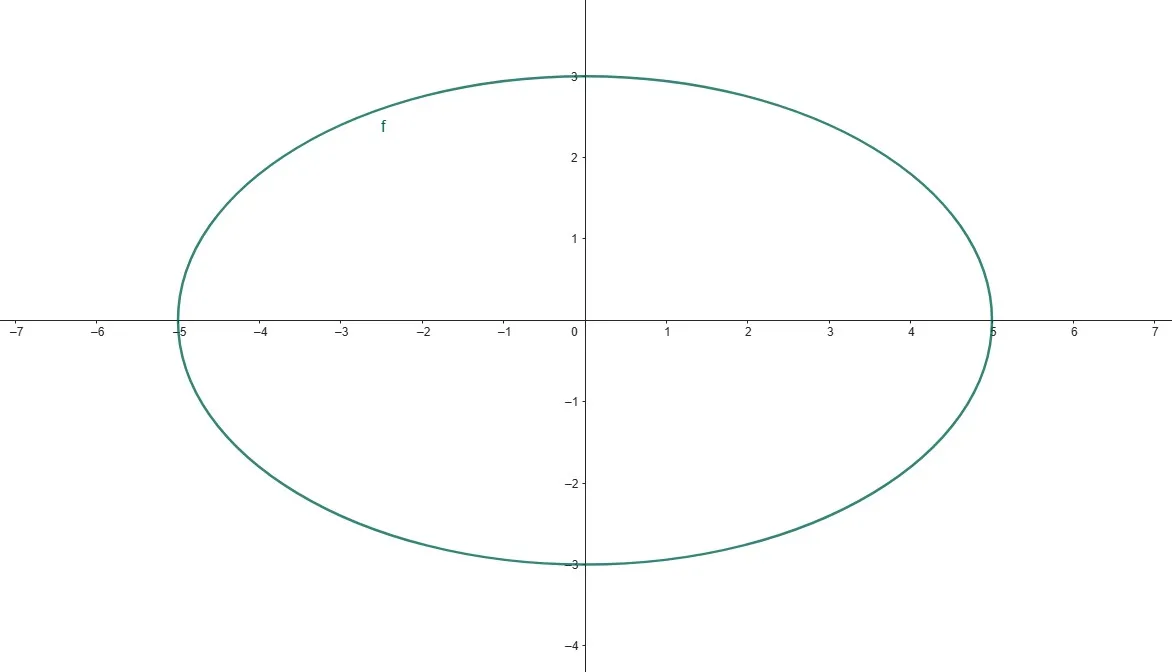
\( \cos(t) = \frac{x}{5} \) и \( \sin(t) = \frac{y}{3} \)
Шаг 2: Подставляем эти выражения в тождество.
\( \left( \frac{y}{3} \right)^2 + \left( \frac{x}{5} \right)^2 = 1 \)
Результат: Уравнение траектории — \( \frac{x^2}{25} + \frac{y^2}{9} = 1 \). Это эллипс.
Пример 3: Экспоненциальная функция (\(e\))
В этом случае на помощь приходит основное свойство логарифма и свойства степеней.
Условие:
\( x(t) = e^t + 2 \)
\( y(t) = e^{2t} + 4e^t + 4 \)
Шаг 1: Выражаем \(e^t\) из первого уравнения.
\( e^t = x — 2 \)
Шаг 2: Замечаем, что второе уравнение является полным квадратом.
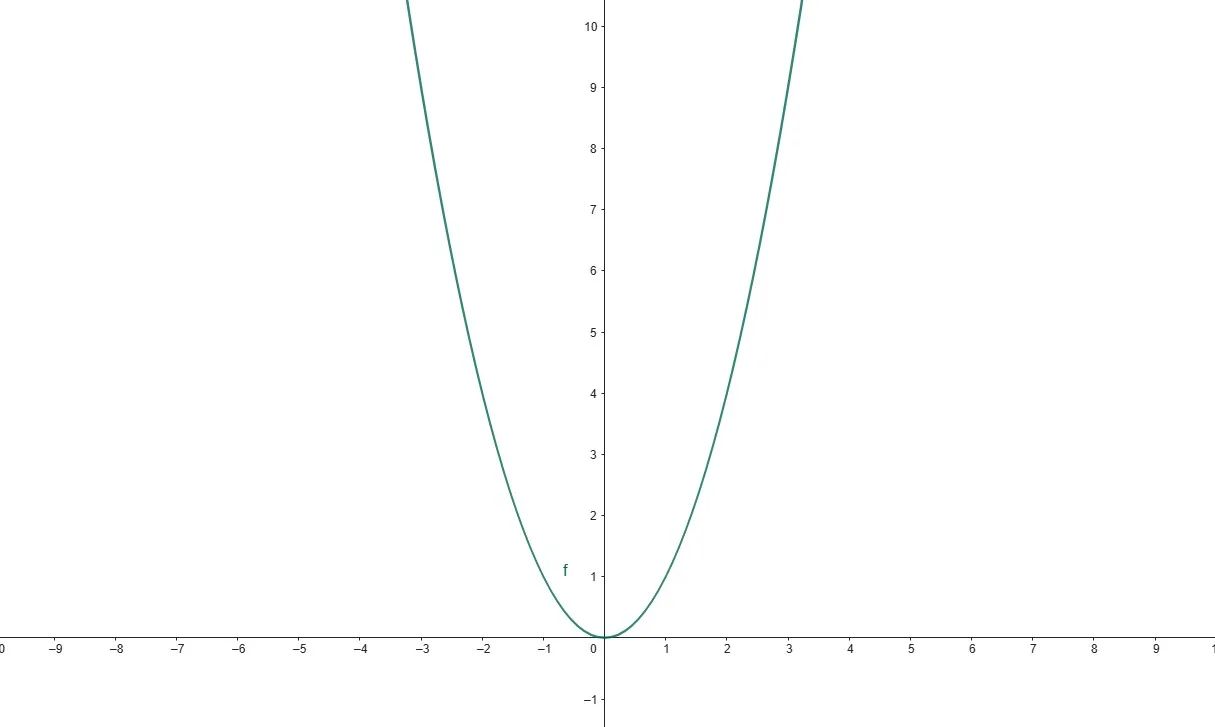
\( y(t) = (e^t)^2 + 2 \cdot 2 \cdot e^t + 2^2 = (e^t + 2)^2 \)
Шаг 3: Подставляем \(e^t\) в \(y(t)\).
\( y = (x-2)^2 + 4(x-2) + 4 = (x^2 — 4x + 4) + (4x — 8) + 4 = x^2 \)
Результат: Уравнение траектории — \( y = x^2 \) (при условии \(x > 2\)).
Когда ничего не получается?
Важно понимать, что не всегда возможно аналитически выразить \(t\). В таких случаях траекторию строят по точкам. Но все кинематические характеристики (скорость, ускорение) все равно можно найти, даже не зная уравнения траектории.
Не хотите заниматься алгеброй?
Наш онлайн-калькулятор не только попытается найти уравнение траектории, но и мгновенно рассчитает все остальные параметры движения, построит график и векторы.
Найти траекторию и выполнить расчет