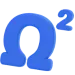Касательное и нормальное ускорение: объясняем на пальцах
Когда машина входит в поворот, ее скорость на спидометре может не меняться, но движение очевидно меняется. Здесь на сцену выходит полное ускорение, которое удобно раскладывать на две ключевые составляющие: касательное и нормальное. Давайте разберемся, что это такое и за что отвечает каждая из них.
Почему одного ускорения недостаточно?
В физике скорость — это вектор, у которого есть величина (модуль) и направление. Ускорение описывает любое изменение этого вектора. Именно для описания этих двух разных типов изменений и ввели два вида ускорения.
Касательное (aτ)
Отвечает за изменение ВЕЛИЧИНЫ скорости.
- Направление: По касательной к траектории.
- Когда возникает: При разгоне или торможении.
- Если \( a_{\tau} > 0 \), движение ускоренное.
- Если \( a_{\tau} < 0 \), движение замедленное.
- Если \( a_{\tau} = 0 \), скорость постоянна.
Нормальное (an)
Отвечает за изменение НАПРАВЛЕНИЯ скорости.
- Направление: Перпендикулярно скорости, к центру кривизны.
- Когда возникает: При любом криволинейном движении.
- Если \( a_{n} > 0 \), траектория искривляется.
- Если \( a_{n} = 0 \), движение прямолинейное.
Формулы и расчет
Полное ускорение \( \vec{a} \) является векторной суммой \( \vec{a} = \vec{a}_{\tau} + \vec{a}_{n} \). Поскольку векторы перпендикулярны, модуль полного ускорения находится по теореме Пифагора.
Модуль полного ускорения:
\( a = \sqrt{a_{\tau}^2 + a_{n}^2} \)
Касательное ускорение (через проекции):
\( a_{\tau} = \frac{v_x a_x + v_y a_y}{\sqrt{v_x^2 + v_y^2}} \)
Нормальное ускорение (через скорость и радиус кривизны R):
\( a_{n} = \frac{v^2}{R} \)
Примеры из жизни для полного понимания
1. Автомобиль на прямой
При разгоне есть только \( a_{\tau} > 0 \). При торможении — \( a_{\tau} < 0 \). Направление не меняется, поэтому \( a_{n} = 0 \).
2. Карусель
Скорость постоянна, значит \( a_{\tau} = 0 \). Но направление постоянно меняется, поэтому есть \( a_{n} > 0 \), направленное к центру карусели.
3. Вход в поворот с торможением
Самый общий случай. Скорость падает (\( a_{\tau} < 0 \)) и траектория искривляется (\( a_{n} > 0 \)). Присутствуют оба вида ускорения.
Сложно считать вручную?
Наш онлайн-калькулятор мгновенно рассчитает для вас и касательное, и нормальное ускорение для любых уравнений движения.
Рассчитать ускорения онлайн