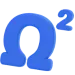Кинематика точки: от основ к практике
Вы когда-нибудь задумывались, как описать движение летящего мяча или движение планеты по орбите? Этим занимается кинематика — раздел механики, который изучает движение тел, не вникая в причины этого движения. В этой статье мы разберем самые основы на простом примере.
Что такое материальная точка?
В физике часто используют упрощение — модель «материальной точки». Это объект, размерами которого можно пренебречь в условиях конкретной задачи. Например, когда мы изучаем движение Земли вокруг Солнца, ее размеры не так важны по сравнению с гигантским расстоянием до Солнца. Поэтому мы можем считать Землю точкой. Это сильно упрощает расчеты.
Ключевые понятия кинематики
Чтобы описать движение, нам нужны три главных «кита», на которых все держится: траектория, скорость и ускорение.
1. Траектория — путь движения
Траектория — это линия, которую описывает точка во время своего движения. Она может быть прямой (прямолинейное движение) или кривой (криволинейное движение). Чаще всего движение точки задается уравнениями, показывающими, как ее координаты X и Y меняются со временем (t): \( x = x(t) \) и \( y = y(t) \). Чтобы найти уравнение траектории, нужно исключить из них время t.
2. Скорость — как быстро и куда?
Скорость — это векторная величина, которая показывает, как быстро меняется положение точки и в каком направлении. Вектор скорости всегда направлен по касательной к траектории. Для нахождения проекций скорости (Vx и Vy) нужно взять производные от уравнений координат по времени.
\( v_x(t) = \frac{dx}{dt} \), \( v_y(t) = \frac{dy}{dt} \)
Модуль полной скорости: \( v = \sqrt{v_x^2 + v_y^2} \)
3. Ускорение — как меняется скорость?
Ускорение — это векторная величина, которая показывает, насколько быстро изменяется вектор скорости. Если точка разгоняется, тормозит или меняет направление — у нее есть ускорение. Проекции ускорения находятся взятием производных от проекций скорости.
\( a_x(t) = \frac{dv_x}{dt} \), \( a_y(t) = \frac{dv_y}{dt} \)
Модуль полного ускорения: \( a = \sqrt{a_x^2 + a_y^2} \)
Разбор простого примера: шаг за шагом
Теория — это хорошо, но давайте посмотрим, как все работает на практике.
Условие задачи
Законы движения точки заданы уравнениями:
\( x(t) = 2t \)
\( y(t) = 4t^2 — 1 \)
Нужно найти все кинематические характеристики в момент времени t = 1 секунда.
Шаг 1: Находим уравнение траектории
Чтобы найти траекторию, исключим время \(t\). Из первого уравнения выразим \( t = x/2 \) и подставим это во второе уравнение:
\( y = 4 \left(\frac{x}{2}\right)^2 — 1 = 4 \frac{x^2}{4} — 1 = x^2 — 1 \).
Результат: Уравнение траектории — \( y = x^2 — 1 \). Это парабола, ветви которой направлены вверх.
Шаг 2: Находим скорость
Найдем проекции скорости, взяв производные: \( v_x = (2t)’ = 2 \) и \( v_y = (4t^2 — 1)’ = 8t \).
В момент времени \( t = 1 \) с: \( v_x(1) = 2 \) м/с, \( v_y(1) = 8 \cdot 1 = 8 \) м/с.
Модуль полной скорости: \( v = \sqrt{2^2 + 8^2} = \sqrt{68} \approx 8.25 \) м/с.
Результат: Скорость точки составляет примерно 8.25 м/с.
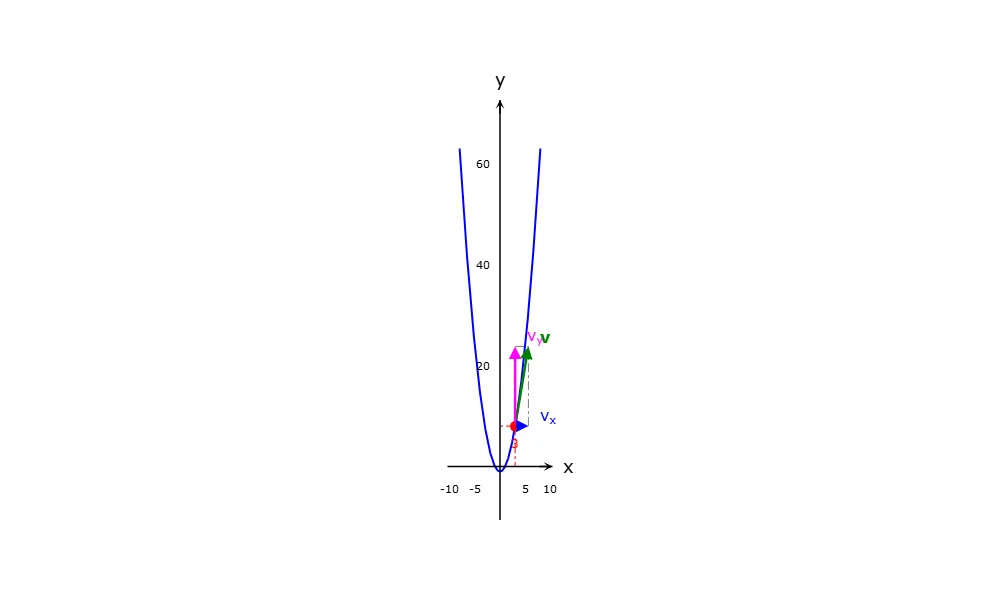
Шаг 3: Находим ускорение
Возьмем производные от проекций скорости: \( a_x = (2)’ = 0 \) и \( a_y = (8t)’ = 8 \).
Проекции ускорения в данном случае постоянны.
Модуль полного ускорения: \( a = \sqrt{0^2 + 8^2} = 8 \) м/с².
Результат: Полное ускорение точки постоянно и равно 8 м/с².
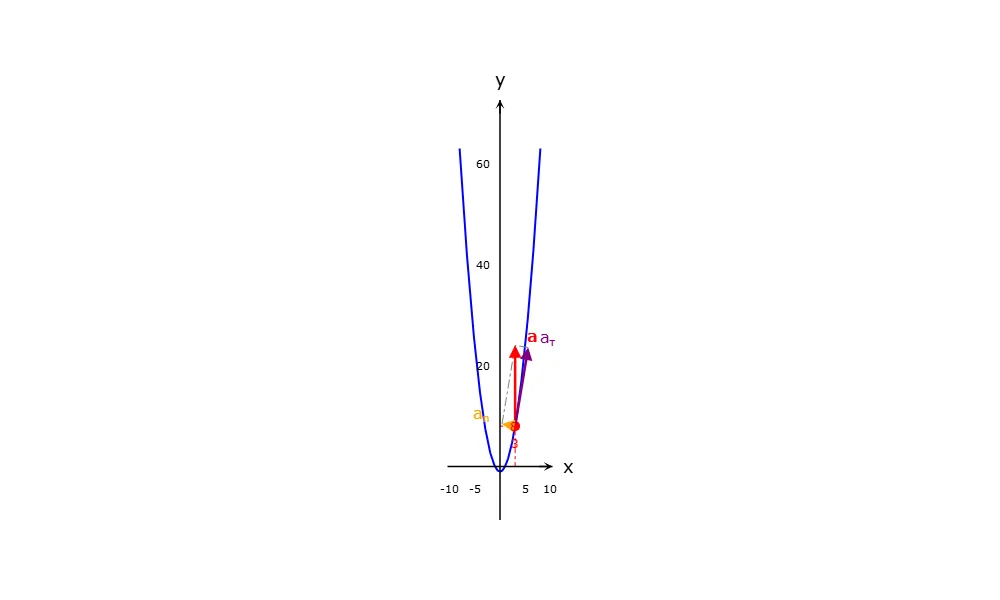
Дополнительно: касательное и нормальное ускорения
Полное ускорение можно разложить на две составляющие: касательное \( a_{\tau} \) (изменение величины скорости) и нормальное \( a_{n} \) (изменение направления скорости). Для нашего примера в момент \( t=1 \) с:
- \( a_{\tau} = \frac{v_x a_x + v_y a_y}{v} = \frac{2 \cdot 0 + 8 \cdot 8}{\sqrt{68}} \approx 7.76 \) м/с². Так как \( a_{\tau} > 0 \), движение ускоренное.
- \( a_{n} = \sqrt{a^2 — a_{\tau}^2} = \sqrt{8^2 — (7.76)^2} \approx 1.95 \) м/с². Так как \( a_{n} > 0 \), траектория криволинейная.
Что в итоге?
Как видите, зная лишь законы изменения координат \( x(t) \) и \( y(t) \), мы можем получить полную картину движения точки: ее путь, скорость, ускорение и характер движения. Это и есть основная задача кинематики. Расчеты вручную могут быть утомительными, но для этого и создаются онлайн-инструменты.
Устали считать вручную?
Наш инструмент для Кинематический анализ движения точки онлайн сделает все расчеты за вас.
Перейти к онлайн-калькулятору