Решение задач динамики: Уравнение Лагранжа второго рода
Рассматривается движение механической системы с одной степенью свободы. Цель — составить дифференциальное уравнение движения, используя мощный аналитический подход, основанный на вычислении кинетической энергии системы и обобщенной силы.
Дано:
- Конфигурация системы (набор тел).
- Массы (m), радиусы (R, r), радиусы инерции (ρ).
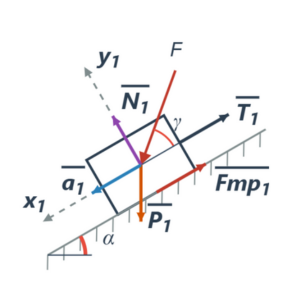
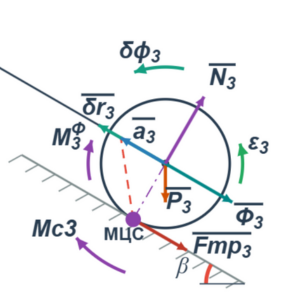
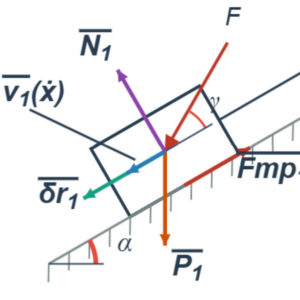
- Действующие внешние силы (F) и моменты (M).
- Наличие сил трения (Fтр) и моментов сопротивления (Mс).
Найти:
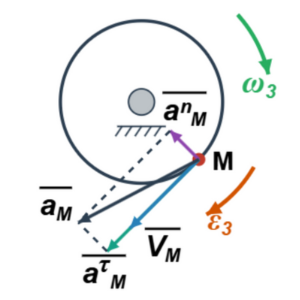
Ускорение (a) или угловое ускорение (ε) указанного тела системы, используя Уравнение Лагранжа второго рода в обобщенных координатах: $$ \frac{d}{dt} \frac{\partial T}{\partial \dot{q}} - \frac{\partial T}{\partial q} = Q $$
Режим: Перемещение
Чтобы получить расчет, сначала постройте расчетную схему.
Заголовок
Сообщение...